离心泵装置工况点的求解有数解法和图解法两种。
一、图解法
图解法简明、直观,在工程中应用较广。
图1为离心泵装置的工况,画出水泵样本中提供的Q-H曲线。再按公式H=Hst+∑h,在沿Hst的高度上,画出管道损失特性曲线Q-∑h,两条曲线相交于M点。此M点表示将水输送至高度为Hst时,水泵供给水的总比能,与管道所要求的总比能相等的那个点,称它为该水泵装置的平衡工况点(也称工作点)。只要外界条件不发生变化,水泵装置将稳定地在这点工作,其出水量为Qm,扬程为Hm。
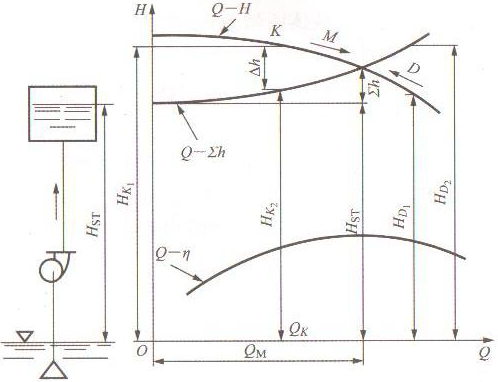
图1 离心泵装置的工况
假设工况点不在M点,而在K点,有图1可见,当流量为Qk时,水泵能够供给水的总比能Hk1将大于所要求的总比能Hk2,也即[供给]>[需要],能量富裕了△h值,此富裕的能量将以动能的形式,使管道中水流加速,流量加大,由此,使水泵的工况点将自动向流量增大的一侧移动,直到移至M点为止。反之,假设水泵装置的工况点不在M点,在D点,那么结果水泵供给的总比能Hd1将小于管道所要求的总比能Hd2,也即[供给]>[需要],管道中水流能量不足,管流减缓,水泵装置的工况点将向流量减小的一侧移动,直到退回M点才达到平衡。所以,M点就是该水泵装置的工况点。如果水泵装置在M点工作时,管道上的所有闸阀是全开的,那么,M点就称为该装置的极限工况点。也就是说,在这个装置中,要保证水泵的静扬程为Hst时,管道中通过的最大流量为Qm。在工程中,我们总是希望水泵装置的工况点能够经常落在该水泵的设计参数值上,这样,水泵的工作效率最高,泵张工作也最经济。
也可以利用折引的方法(也称“折引特性曲线法”)来求该水泵装置的工况点。如图2所示,先沿Q坐标轴的下面画出该管道损失特性曲线Q-∑h,再在水泵的Q-H特性曲线上减去相应流量下的水头损失,得到(Q-H)´曲线。此(Q-H)´曲线称为折引特性曲线。此曲线上各点的纵坐标值表示水泵在扣除了管道中相应流量时的水头损失以后尚剩的能量。这能量仅用来改变被抽升水的位能,即它把水提升到Hst的高度上去。因此,沿水塔水位作一水平线,与(Q-H)´曲线相交于M1点,此M1点纵坐标代表了该装置的静扬程,由M1点向上作垂线引申于Q-H曲线相交于M点,则M点的纵坐标值Hm,即为该水泵的工作扬程Hm=Hst+∑h。它就是管道需要的总比能与水泵供给的总比能正好相等的一点,M点称为该离心泵装置的工况点,其相应的流量为Qm。
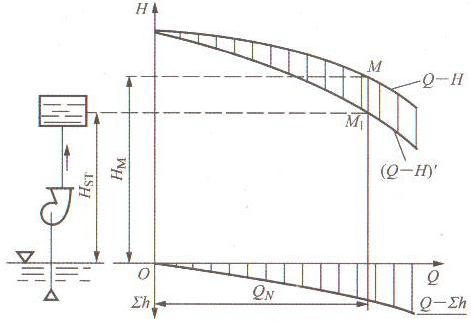
图2 折引特性曲线法求工况点
若水泵的性能曲线上有驼峰形状,则它与管路性能曲线的交点可能出现两个,如图3所示,其中在水泵性能曲线下降段的交点为稳定工作点,其上升段的交点则是不稳定工作点。假若水泵在K点工作,由于某种原因使工作点离开K向右移动,则能量供大于求,流量增加,直到越过顶峰,在下降段某一点(如M点)才稳定下来;反之工作点向左移动,则能量供不应求,使流量减小,直到流量等于零为止。由上述可知,一旦有外界干扰,工作点离开K之后再也不会回到K点。不仅K点,而且整个上升曲线段都是这种情况。因此,水泵性能曲线的上升段是不稳定工作区,泵运行时应避开此区,只有下降段才是稳定工作区。
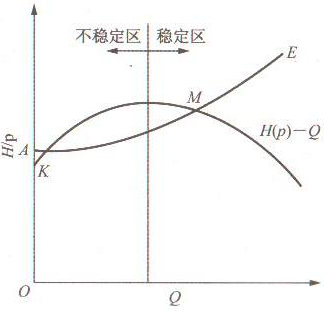
图3 水泵不稳定工作区
二、数解法
离心泵装置工况点的数解,其数学依据是如何从水泵及管道系统特性曲线方程中解出Q和H值,即有下列两个方程求解Q、H值:H=f(Q) (4) H=Hst+∑KQ² (5)
由式(4),式(5)可见,两个方程求两个未知数是完全可能的,关键在于如何来确定水泵的H=f(Q)函数关系。
现假设水泵厂样本中所提供的Q-H曲线上的高效段,可利用下列方程的形式来表示:H=Hx-hx (6)
式中:H为水泵的实际扬程(m):
Hx为水泵在Q=0时所产生的虚总扬程(m),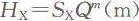 ; ;
hx为相应于流量为Q时,泵内的虚水头损失之和;
Sx为泵体内虚阻耗系数;
m为指数。对给水管道一般m=2或m=1.84。
现采用m=2,则得H=Hx-SxQ² (7)
图4为式(7)的图示形式,它将水泵的高效段视为SxQ²曲线的一个组成部分,并延长与纵轴相交得Hx值。然后,在高效段内任意选择两点的坐标,代入式(7),此两点一定能满足此方程式,即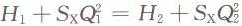
对于一台水泵而言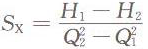 (8) (8)
因H1、H2,Q1、Q2均已知值,故可以求出Sx值。将式(8)代入式(7)可得:Hx=H1+SxQ² (9)
由式(9)可以求出Hx值。表1列出了SA型号离心泵的Hx、Sx值。根据这些数据,就可以写出水泵的Q-H特性曲线方程式:H=Hx-SxQ² (10)
表1 SA型号离心泵的Hx及Sx值
|
水泵型号
|
转速(r/min)
|
叶轮直径(mm)
|
m=2
|
|
Hx/m
|
Sx(s/L) ²/m
|
|
6SA-8
|
2950
|
270
|
112.76
|
0.00715
|
|
6SA-12
|
2950
|
205
|
61.67
|
0.00407
|
|
8SA-10
|
2950
|
272
|
107.40
|
0.00233
|
|
8SA-14
|
2950
|
235
|
79.41
|
0.00288
|
|
10SA-6
|
1450
|
530
|
100.43
|
0.000286
|
|
14SA-10
|
1450
|
466
|
76.25
|
0.0001
|
|
16SA-9
|
1450
|
535
|
105.19
|
0.000075
|
|
20SA-22
|
960
|
466
|
29.54
|
0.000028
|
|
24SA-10
|
960
|
765
|
92.13
|
0.0000234
|
|
28SA-10
|
960
|
840
|
115.67
|
0.0000151
|
|
32SA-10
|
585
|
990
|
59.29
|
0.00000529
|
|
湘江56-23
|
375
|
1200
|
30.29
|
0.00000042
|
|
12Hдc
|
1450
|
460
|
76.50
|
0.0001
|
|
14Hдc
|
1450
|
529
|
102.90
|
0.000088
|
|
20Hдc
|
960
|
765
|
92.90
|
0.000024
|
当离心泵工作时,由式(5)及式(10)可得:Hx-SxQ²=Hst+∑KQ²
也即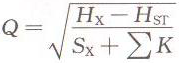
式中Hx、Sx及∑K均为已知值,当Hst一定时,即可求出水泵相应工况点的流量和扬程。
上述方程式(10)的建立,是把水泵的高效段视为二次抛物线上的一段。采用这种方式来建立Q-H特性曲线方程,称为抛物法。但是,实际上并不是每台水泵的高效段均能满足假设条件的。这样,在实际采用中就会存在一定的误差。
拟合离心泵Q-H曲线方程的另一途径是采用最小二乘法来进行。我们将高等数学中的最小二乘法引用与离心泵Q、H的双变量关系中,其正方程组可写成:.png) (12a) (12a)
拟合离心泵的Q-H特性曲线方程可按下式求得:H=H0+S1Q+S2Q² (12b)或H=H0+S1Q+S2Q²+S3Q³ (12c)
方程式(12b)一般用于手算,式(12c)精度较高,可用于电算。
例1 现有14SA-10型离心泵一台,转速n=1450r/min,叶轮直径D=466mm,其Q-H特性曲线如图5所示。试拟合Q-H特性曲线方程。
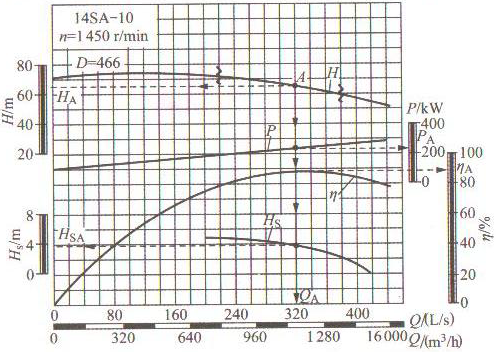
图4 14SA型离心泵的特性曲线
解 在14SA-10型的Q-H特性曲线上,取包括(Qo、Ho)在内的任意四点,其值如表2所示。上表中H值单位为m;Q值单位为L/s。
表2 四个工况点的(Q、H) 值
|
型号
|
已知各点的坐标值
|
代数计算值
|
|
Ho
|
Qo
|
H1
|
Q1
|
H2
|
Q2
|
H3
|
Q3
|
S1
|
S2
|
|
14SA-10
|
72
|
0
|
70
|
240
|
65
|
340
|
60
|
380
|
0.0168
|
-0.000117
|
将已知的各坐标值代入式(12a),可得:
将上式简化后,解得:S1=0.0168; S2=-0.000117
将结果S1、S2值代入式(12b),得该水泵的Q-H特性曲线方程为
H=72+0.0168Q-0.000117Q²
将上式与该水泵装置的管道特性曲线方程式(5)联立,即可求得其工况点的Q、H)值。 |